The Looming Problem of Slow & Brittle Proofs in SMT Verification (and a Step Toward Solving It)
dafny proofs verification proof_localisation smt
All is not well in the land of automated formal verification.
Automated verification tools and programming languages such as Dafny or Viper provide a tempting alternative to traditional manual verification: by delegating proof obligations to an SMT solver, developers can instead focus on the code itself and do not need to busy themselves with writing proofs.
// An example [verified] dafny program; max of two numbers
method max(a: int, b: int) returns (m: int)
requires a >= 0 && b >= 0 // pre-post condition
ensures m >= a && m >= b {
if (a > b) { m := a; } else { m := b; }
}
Tools like Dafny and Viper are increasingly used in industry (AWS, Microsoft etc.), and now form a core part of pipelines used for verifying safety-critical software in practice. Sadly, as they've been applied to larger codebases, people are increasingly noticing a worrying trend: slow and brittle proofs.
Proof brittleness: When verification times for a program become slow and erratic, and seemingly irrelevant changes (such as renaming variables) can even cause verification to fail.
At its core, this issue arises primarily from the SMT solver itself, as the success of a verification run may have inadvertently been dependent of some irrelevant feature of the program affecting the proof search, and while this seems minor, it can severely hamper usability and practicality of these tools:
- If proofs are slow, each time a file is reopened (on a new device or shared with another user), developers will have to wait up to hours to get feedback.
- If proofs are brittle, then integrating verification into CI may lead to spurious verification failures, as periodically proofs may randomly stop working after changes.
Indeed, if we look at active verification projects (Daisy-NFSD: a verified file-server), we can see that developers do actively care about this brittleness and proof slowdown, and a fair amount of effort is spent avoiding it:
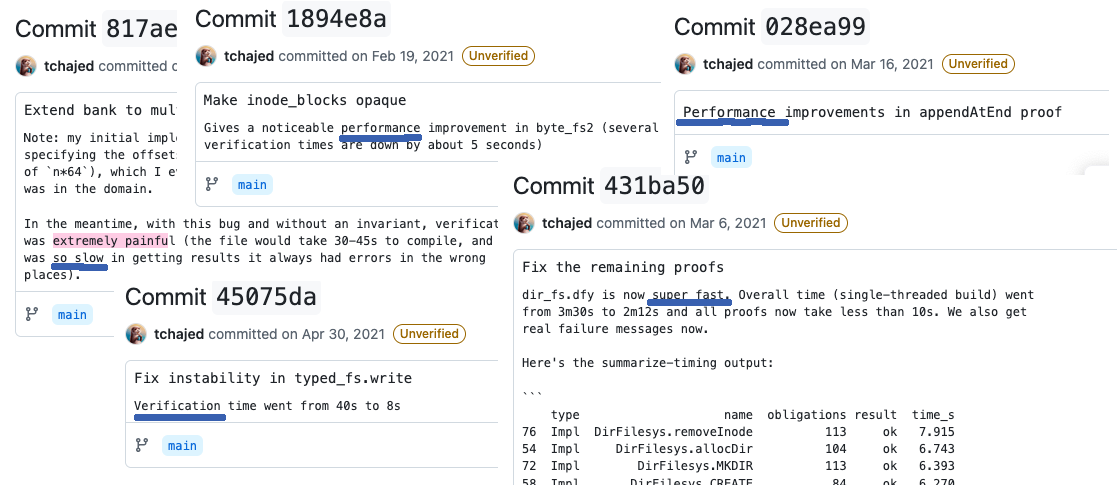
But this manual approach is clearly unscalable. Can we do better?
In today's blog post, I'm going to be talking about some cool research that I've done recently (to be presented at CAV next month1), towards an automated solution to this problem!
TL;DR: by cleverly exploiting internal details of SMT solvers, we were able to produce a tool that could "localise" automated proofs to reduce verification times especially so for slow programs (up to 1000x):
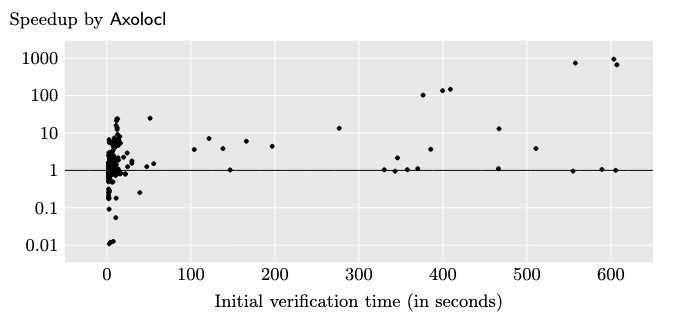
You can check out the full paper here: pdf, or the artefact for the implementation here: code.
A Primer on SMT-based Verification
Let's start by a quick overview on how SMT based verifiers work!
Here's a simple function in Boogie (the underlying language that both Dafny and Viper compile to):
procedure test(x: Seq, y: Seq) returns (res: Seq)
requires NonEmpty(x) /\ NonEmpty(y);
ensures NonEmpty(res) {
res := Append(x,y);
}
It's a simple dummy function that takes in two sequences, with a
precondition that both sequences should be non-empty, and then returns
the result of calling Append on both, with a
postcondition asserting that the result is also non-empty.
During compilation, for each procedure, the verification annotations are used to produce a logical formula that will check the correctness of the program2:
\begin{gather*} BG \wedge (\text{NonEmpty}(x) \wedge \text{NonEmpty}(y)) \Rightarrow \text{NonEmpty}(\text{Append}(x,y)) \end{gather*}
In this case, the formula states that the preconditions of the
function NonEmpty(x) /\ NonEmpty(y),
conjoined with some background theory BG,
will imply the postcondition NonEmpty(Append(x,y)). That is, in other words, that if the
precondition is satsfied, then the postcondition holds after the
program runs.
The background theory in this case is constructed from previous declarations and axioms in the file defining any types and functions used in the program:
type Seq;
const Nil: Seq;
function Append(l: Seq, r: Seq): Seq;
function NonEmpty(l: Seq): bool;
function Length(l: Seq): int;
axiom (forall l: Seq, r: Seq ::
NonEmpty(Append(l,r)) = (NonEmpty(l) \/ NonEmpty(r)));
axiom (forall s: Seq ::
(Length(s) > 0) = NonEmpty(s));
These formulae (called verification conditions) are sent to an SMT solver, which then returns a binary yes or no answer certifying the program, after which compilation can proceed as normal.
How to prove it; SMT-style
Now the full details of how the SMT solver proves a logical formula holds is outside of scope for this post, but at a high level you can think of a substantial part of the proof effort being in instantiating quantifiers.
For example from our earlier logical formula:
\begin{gather*} BG \wedge (\text{NonEmpty}(x) \wedge \text{NonEmpty}(y)) \Rightarrow \text{NonEmpty}(\text{Append}(x,y)) \end{gather*}If we pick this quantified axiom in our background theory:
\[ \forall a, b, \text{NonEmpty}(\text{Append}(a,b)) = \text{NonEmpty}(l) \vee \text{NonEmpty}(r) \]
We can instantiate this with \(a \mapsto x\) and \(b \mapsto y\) to simplify our verification condition to the following:
\[ BG \wedge (\text{NonEmpty}(x) \wedge \text{NonEmpty}(y)) \Rightarrow \text{NonEmpty}(x) \vee \text{NonEmpty}(y) \]
At this point, our VC effectively corresponds to the following propositional formula:
\[ A \wedge B \Rightarrow A \vee B \] and this can be proven using standard techniques.
The real challenge in this proof is choosing the right quantifier instantiations to choose – if we instantiated our quantified formulae with \(a \mapsto \text{Append}(x,y)\), then we would not have made any progress in our proof. In a real program there may be many such candidates, both quantified formulae and arguments to instantiate, that the SMT solver could pick, and so a substantial portion of verification time is actually spent in exploring different quantifier instantiations.
Because this makes up such an important part of the solver's proof search, SMT solvers actually also provide a mechanism for tuning the heuristics they use for performing quantifier instantiation, called triggers.
axiom (forall l: Seq, r: Seq ::
/* trigger: */ {NonEmpty(Append(l,r))}
NonEmpty(Append(l,r)) = (NonEmpty(l) \/ NonEmpty(r)));
In the above statement, the trigger NonEmpty(Append(l,r)) can be thought of effectively as a sort
of "pattern" – an expression that uses one or more of the quantified
variables.
Effectively, the semantics of this constraint are to inform the SMT
solver to only instantiate the axiom if it can match the pattern to
some part of it's internal state. So for example, if the SMT solver
had the expression NonEmpty(Append(Nil, Nil))3 in the context somewhere, then the pattern would match and the
quantifier would be instantiated binding \(l \mapsto Nil\) and \(r
\mapsto Nil\).
A technique to reduce verification times: Proof Localisation
In this work, we decided to try and optimise verification times by tackling this particular problem: is there some way of making proofs faster by reducing the number of quantifier instantiations?
As it turns out, the answer to this is yes! and not only can this be done, we can do it purely using the existing constructs exposed by verification tools, without requiring any changes to the SMT solver or the verifier.
We dubbed this technique "proof localisation", and the core of this approach relies on two components:
- UNSAT Cores
- Guarded Axioms
Let's go through these one by one, starting with UNSAT cores.
Modern SMT solvers actually provide a lot of additional information beyond just a yes or no answer to the validity4 of the submitted logical formulae and if queried can produce helpful information about the proof search it used to produce a conclusion. One such feature are UNSAT cores, which effectively give a list of all axioms that ended up being used to prove the property. If we knew exactly which subset of axioms were needed to prove a goal, then we could be able to reduce verification times by asking the SMT solver to restrict which quantifiers it considered to instantiate to just these ones.
Now, assuming we have a list of the useful axioms for a proof, how can we enforce the SMT solver only considers these for instantiation? This brings us on to the first contribution of this work: Guarded Axioms. As it turns out, we can actually exploit the mechanism of triggers to perform this kind of restriction.
The core idea is to create artificial functions to "guard" uses of an axiom:
// create a guard function
function guard1(b: bool): bool;
// guarded axiom
axiom (forall b: bool :: {guard1(b)},
(forall l: Seq, r: Seq ::
/* trigger: */ {NonEmpty(Append(l,r))}
NonEmpty(Append(l,r)) = (NonEmpty(l) \/ NonEmpty(r)))
);
Here, we introduced the symbol guard1, and
then modified our axiom by wrapping it in another quantifier, placing
a trigger on it such that this axiom can only be instantiated if the
guard function is present. As this symbol is fresh5 we now have
full control over where the SMT solver can consider using this function.
Now, in order to "enable" this axiom before an assertion, we can simply assume the guard function:
// enable the guard function
assume guard1(true);
// assert the thing you want to prove
assert NonEmpty(Append(l,r));
In order to precisely scope the enabling of each axiom we can use a sort of non-deterministic branch:
// branch the verification
if(*) {
// enable axiom
assume guard1(true);
// prove property
assert NonEmpty(Append(l,r));
// terminate verification
assume false;
}
// in other branch, assume property
assume NonEmpty(Append(l,r));
The idea here is that when the verifier enters the first branch it will enable the axiom and prove the property but then hit the assume false after which it can terminate that branch early, and in the other branch it can simply assume that the property holds without verification as it has been proven in the previous one.
Combining these techniques, I implemented a modified version of the Boogie verification tool that automatically computed their UNSAT cores and then rewrote each assertion to be guarded and explicitly enable the axioms it depended on – automatic proof localisation? not quite…
Instantiation Graphs & Lurking Axioms
Sadly, the story didn't quite end there, and when we moved to actually check the verification times of these rewritten programs, we found that the programs were now failing to verify.
As it turns out, UNSAT cores are actually incomplete: but not in an unsound way!
The results from the SMT solver did indicate all the logically relevant axioms that were needed for the proof, but it turns out that this list doesn't capture all the facts that are needed for a proof to go through — as it turns out, there's an entire class of additional axioms that I discovered that are missed: Lurking axioms.
Lurking axioms – axioms in an SMT query that are logically irrelevant to the goal being proven but in practice are required for the proof to succeed.
How can this be possible? Well, it once again all comes back to our old friend, triggers and quantifier instantiations.
Let's go back to our program from before, but let's consider a different set of triggers for these axioms:
axiom (forall l: Seq, r: Seq :: {Length(l), Length(r)}
NonEmpty(Append(l,r)) = (NonEmpty(l) \/ NonEmpty(r)));
axiom (forall s: Seq :: {NonEmpty(s)}
(Length(l) > 0) = NonEmpty(l));
Here, we've set the trigger for the first axiom to be
Length(l) and Length(r), and the trigger for the second axiom to be
NonEmpty(s).
Now the problem here is that if we're trying to prove the verification condition from before:
\begin{gather*} BG \wedge (\text{NonEmpty}(x) \wedge \text{NonEmpty}(y)) \Rightarrow \text{NonEmpty}(\text{Append}(x,y)) \end{gather*}
Then the only logically relevant axiom, and the axiom that will show
up in the UNSAT core, is axiom 1 as before. But if we try to verify
our program with only this axiom, then verification would fail, as the
SMT solver would never have the term Length(x) or Length(y) in its
context. If we include both axioms, then axiom 2 acts as a lurking
axiom: it gets instantiated during the proof search, and introduces a
term of Length(x), Length(y) into the
context, which can then enable the SMT solver to instantiate the
logically relevant one.
Long story short, if we want our proofs to go through, then it is not only necessary to include the axioms in the UNSAT core in our localised programs, but we must also capture lurking axioms, but how can we do this?
This brings us to the final key idea in this work, which is to exploit SMT traces! SMT solvers, such as Z3, can be instructed to produce a log of all the quantifier instantiations they make during the proof search – tools such as ETH-Zurich's Axiom Profiler can use this information to produce a graph of all the instantiations made during the proof search:
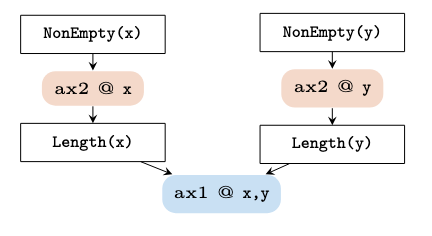
Here this graph represents the instantiations that were made in order to instantiate axiom 1 with x and y. The shaded boxes represent instantiations of axioms, the square boxes are terms in the SMT solver's context, and arrows denote dependencies between the two. From the graph, we can see that in order for the logically relevant axiom to be instantiated, it depended on terms produced by the lurking axiom.
Putting it all together, in the final tool, alongside the axioms from the UNSAT core, we extract the instantiation graph as well, and perform a breadth-first search to also include the necessary lurking axioms as well, and thereby were able to automatically rewrite Boogie programs to reduce their verification times.
Conclusion
By delegating proof obligations to an SMT solver, automated tools reduce the burden on users and take great steps towards making verification practical and mainstream, but at the same time, as we have seen, this dependence on SMT is a blessing and a curse.
In this work we've looked at improving proof maintenance of these kinds of systems by reducing verification times, and in the process we've taken a short detour through automated verification tools, SMT solvers, and some fun internal details of SMT solvers that turn out to be essential for optimising proofs.
In the paper (here), we evaluated this tool, AXOLOCL, on a number of real industrial verification codebases, including AWS' verified cryptographic libraries, the formalisation of the CEDAR policy language and a few other active codebases, and compared the verification times before and after localising them using AXOLOCL:
| Suite | Total LOC | Mean Time (s) | Time Before (s) | Time After (s) | Speedup |
| AWS | 1,264,497 | 16 | 370 | 380 | 1.0 |
| Dafny-VMC | 10,916 | 2 | 2 | 2 | 1.0 |
| Cedar | 1,198,291 | 64 | 967 | 349 | 2.8 |
| Daisy-NFSD | 109,801 | 7 | 69 | 50 | 1.4 |
| EVM | 548,790 | 9 | 141 | 131 | 1.1 |
| Viper | 63,790 | 181 | 3,070 | 711 | 4.3 |
| Komodo | 26,371 | 9 | 45 | 15 | 3.0 |
| VeriBetrKV | 6,718,495 | 23 | 6,569 | 5,757 | 1.1 |
As I've shown earlier, a lot of actively developed projects have already had a substantial portion of developer time invested into already hardening and optimising proofs manually, so for fast projects, we had minimal improvements, but for brittle and slow ones we were able to reduce aggregate verification times across the whole codebase by up to 4x, making the systems substantially more practical.
Footnotes
Sadly I will not be able to present it myself due to not wanting to risk visa issues, thanks Trump~
I've taken some strong creative liberties for simplifying the exposition here: actually, because of how SMT solvers work (they produce satisfying assignments), the actual VC is a sort of negation of this formula so that failure to find a satisfying assignment (UNSAT) corresponds to verification success.
The astute reader may have noted that NonEmpty(Append(Nil,Nil)) logically shouldn't hold; this is
correct! An important thing to note is that the pattern for a trigger
doesn't need to match something the SMT solver has shown is true, it
just needs to match any expression the SMT solver may know about,
which includes expressions that the SMT solver thinks don't hold as
well.
Again, for ease of exposition, using validity here, where in practice the whole thing is flipped and we query satisfiability/unsatisfiability.
I.e it won't occur in the codebase unless we put it there.