Friendship ended with Monads: Testing out Algebraic effects in OCaml for Animations

Warning Tihs post was written a long time ago, before I began my transition. This warning is included to inform you that this post adopts a tone that I no longer feel is appropriate and that the page may make use of design that is not consistent with the rest of the site.

Friendship ended with Monads: Testing out Algebraic effects in OCaml for Animations
01 Jan, 2021 ocaml effects animations game

Recently, I had the pleasure of talking with KC Sivaramakrishnan - one of the lead developers of the OCaml multicore project - when he came to NUS to give us a talk on his work on multicore and a potential new language feature for OCaml: Algebraic effects. At a high level, the run-down on algebraic effects is that they can be considered as a sort of alternative to monads,¹^,² however with the key benefit that they play a lot nicer with existing direct-style code and thus might be a more fluid and ergonomic tool. One of my most surprising takeaways from meeting KC was in realising the significant amount of progress that had already been made on implementing algebraic effects in OCaml - in fact, algebraic effects, far from just being a far-off pipe-dream (cough, modular implicits, cough), are actually at a point where it is possible (fairly easy even) to play with them right now (albeit using an experimental fork of the OCaml compiler).

Indeed, this is exactly what I have been working on over the past few weeks - so moved was I by the world of possibilities opened up by this development, I immediately set about experimenting on inserting algebraic effects into various OCaml projects that I happened have handy at the time. Over the course of these experiments, I ended up considering the application of algebraic effects to functional game development, and in the process stumbled upon a rather elegant pattern for representing animations in a functional style. In fact, this pattern actually ended up solving a longstanding issue I was having with managing the control flow for animations alongside game logic, and so I think it forms a rather nice setting for exploring the benefits of algebraic effects, hence this post.

In the rest of this blog post, I'm going to provide a gentle introduction to algebraic effects, provided in the context of their use in implementing functional game animations - we'll look at using algebraic effects to implement 3 different case studies of relatively complex animations (see above) for games in a fluid and elegant way. Hopefully, through exploring these case-studies, you should be able to gain a better understanding of the pros and cons of algebraic effects and why they are certainly something to be excited about.

The executable code for the entire blog post can be found at:³ https://gitlab.com/gopiandcode/ocaml-game-animations-with-algebraic-effects

The vision: Functional Game Development

While our final code uses a mix of functional and imperative code (as is idiomatic OCaml style), our journey really begins in the world of pure functional games.

Fundamentally, functional games work by separating the execution of a game into two distinct functions representing the main phases of the game loop:

an update function that takes user input and time and updates the state of the world
a draw function that displays the current state of the world to the screen.

The idea here is that while the state of the game may change over time, the individual update and draw functions are pure and referentially transparent, and thus come with all the usual benefits of functional code (modularity and compositionality, reusable code, easier to reason about etc.).

To see these ideas in practice, suppose we wanted to implement a simple menu for a game:

Following the functional approach, we could define the state of our menu as follows:

type menu = { selected: int; options: string list; }

Using this fairly simple state, we can easily write a pure draw function for the menu as follows:


let draw_item ~pos ~is_active txt = ... (* draw an individual menu item *)

let draw {selected;options} =
    List.iteri (fun ind option ->  
       draw_item ~pos:ind ~is_active:(ind = selected) option
    ) options

Similarly, if we wanted to make the menu respond to user inputs, we can write a functional update operation for the menu as follows:

let update menu key = 
   let len = length menu.options in
   let next pos = (pos + 1) mod len in
   let prev pos = (pos - 1 + len) mod len in
   match key with
   | Up -> {menu with selected = next menu.selected}
   | Down -> {menu with selected = prev menu.selected}

Hooking these all up together, the main loop for our program might then look as follows:

let main () : unit = 
   let rec loop menu = 
      draw menu;
      let input = get_input () in
      let menu = update menu input in
      loop menu in
   loop {selected=0; options=["A"; "B"; "C"]}

And tada! We now have a fully functional menu that dynamically responds and updates to user inputs, and we were able to do it all without having to ever dirty our hands with any evil impure code.

Functional game development sounds great, right?

The challenge: Managing animations

The stuff that I presented in the previous section is nothing new - there are countless prior blog posts and videos on the web that all describe this style of a game engine, and it paints a very pretty picture.

Unfortunately, I am afraid to say, not all is as it seems in the land of functional game development, and when you start using this methodology to develop any kind of non-trivial games, you can quickly find yourself running into edge-cases, and one particularly nefarious example of such issues is handling animations.

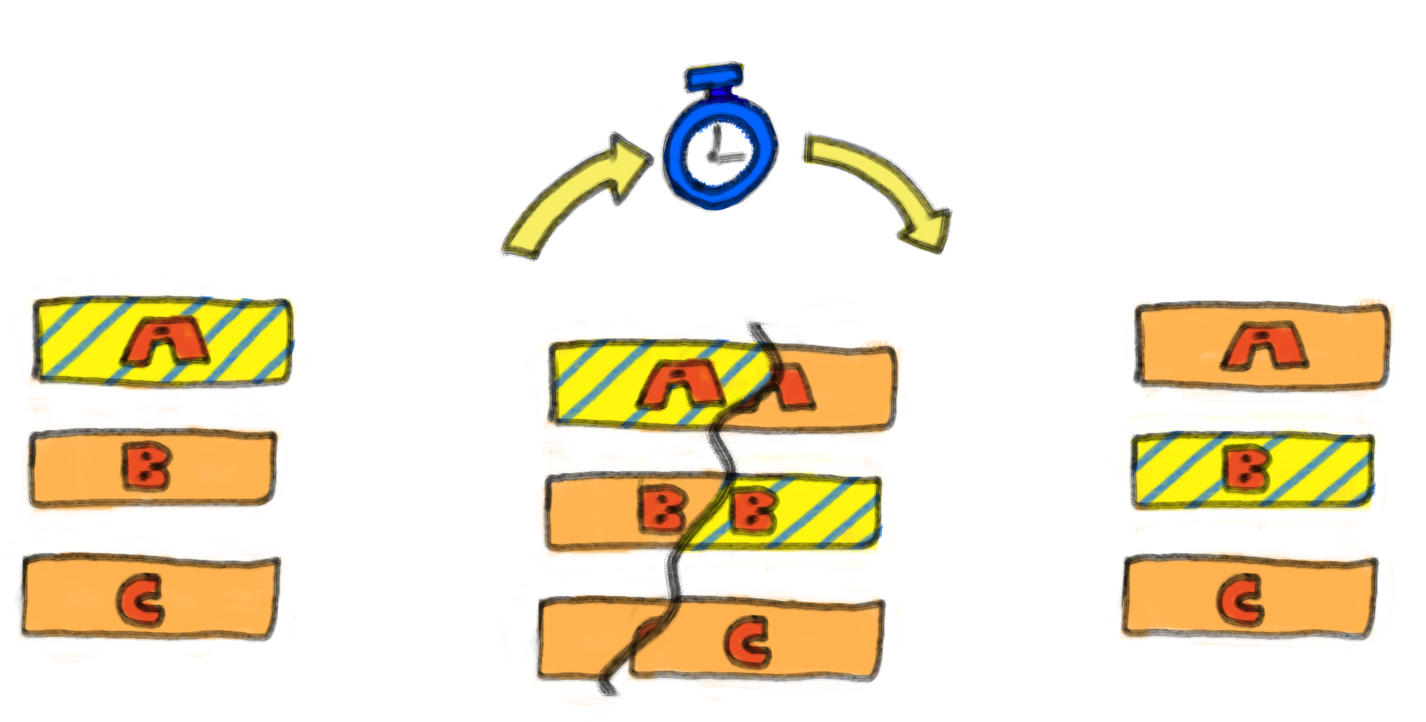
Returning back to our running example of a game menu, suppose we now wanted to come back and add a simple quality of life feature to our menu - nothing complex, just a fade-in between states of the menu.

In other words, when the user presses a button, there should be small time-delay as the menu gradually transitions from the original state to the new one:

Okay, sure - that's not a complex transformation - so this should be simple to implement within our framework, right?

Unfortunately, no.

Our methodology so far was based entirely around the assumption that the update function is pure and stateless and should be called on each frame of the game.

As such, if we were to return a new menu with the next item selected when the user presses down, the transformation would be immediate rather than the gradual change we want.

So what exactly should we return from our update function then?

If one were to strictly adhere to the functional game development paradigm, then one hacky way to achieve this would be to explicitly track the state of animations in the menu.

For example, we can update our definition of menu to be as follows:

type time = int
type state = Static of int | MovingBetween of int * int * time
type menu = { selected: state; options: string list; }

The idea here is that the state type tracks the two possible states of the menu and its animations:

either the animation is complete and the menu is static
or the menu is in the middle of an animation between two states with some amount of time (in ms) remaining.

With this change, we can then write our update function as follows (now updated to take an additional time parameter tracking the time between frames):

let update menu key delta = 
  let len = length menu.options in
  let next pos = (pos + 1) mod len in
  let prev pos = (pos - 1 + len) mod len in
  match menu.state with
  | MovingBetween (old_ind,new_ind, remaining) ->
    let remaining = remaining - delta in
    if remaining < 0 (* is animation completed? *)
    then {menu with selected = Static new_ind} (* yes: return to static *)
    else {menu with selected = MovingBetween (old_ind, new_ind, remaining)}
  | Static ind ->
    match key with (* only process inputs when animations completed *)
    | Up -> {menu with selected = MovingBetween (ind, next menu.selected, 100)}
    | Down -> {menu with selected = MovingBetween (ind, prev menu.selected, 100)}

So this will work decently well, however, we're now starting to mix our animation code with the logic of the program, making it harder to understand and also more probable for bugs to creep in. Additionally, while this happens to work for our simple example, the pattern isn't scalable - adding more animations would require rewriting the entire function.

Clearly, taking this purely functional approach to games development has some serious difficulties with managing animations, but it would be unfair to say that this is uniquely due to the functional approach:

The challenge of balancing animations flow with logic is inherent to the domain

For the rest of this blog post, we'll shift gears to investigate how algebraic effects can be used to implement animations when dealing with a slightly more imperative game structure, however this is mainly to simplify the implementation: the core ideas presented below can be easily ported to a pure implementation.

Algebraic effects to the rescue

Taking a step back from our previous example, the fundamental issue was that we were trying to mix two separate threads of control - one for the core logic, and a separate one for the animation - in other words, what we need is some kind of non-local control flow.

….as it just so happens, this is exactly the functionality that algebraic effects provide.

What are algebraic effects?

We'll sidestep a more detailed discussion of the theory, and instead focus on the general picture for the end user: algebraic effects as effectively "resumable" exceptions.⁴

When defining an effect, the user specifies the type of the input supplied by the caller, and the type of the output that the effect should return on completion:

effect A : int -> float

To perform an effect, we can use the builtin primitive perform:

perform (A 1)

At this point, the execution of the current program is stopped (much like an exception), and control changes up the stack until the nearest effect handler:

try 
   ...
   perform (A 1)
   ...   
with 
  | effect (A v) k ->
    (* control changes to here *)

At the site of the effect handler, the user receives the parameter passed to the effect and also a continuation k that can be invoked using the continue primitive to resume the program:

continue k 1.0

Here, the parameter passed to the resume the continuation must match the type specified at the declaration of the effect.

Putting it all together, the control flow of an OCaml program with effects would look like this:


let () = 
   try 
      let x = perform (A 1) in (* -1-+       *)
      x +. 1.0          (* <----------|----+  *)
   with                (*            |    |  *)
   | effect (A v) k -> (* <----------+    |  *)
      continue k 1.0   (* --2-------------+  *)

While this may seem at first like a rather contrived functionality, it turns out to be perfect for implementing animations.

Implementing animations with Algebraic effects

With the power of algebraic effects at our hands, we now have the ability to fluidly represent non-local control flow in OCaml, and so we can start moving towards constructing an interface for animations.

What's in an animation?

Before we start writing any code, it is important to first clarify the kinds functionalities and features we actually need to support in our interface.

From my experience, there are three main kinds of features that code using animations often rely on:

1. A composable language of timelines - Complex animations are not typically just atomic units of computation, but rather are usually constructed out of smaller, simpler animations - these compositions are most naturally expressed in the language of timelines.

As such, to allow constructing complex animations with ease, our interface for animations should have primitives to allow composing animations into more complex ones, such as:
- Composition in parallel
- Composition in sequence
Separating animations with delays
2. Independent control flow - The other key component of animations is that they should have an independent control flow - as we saw in our running example, we want to decouple the execution of the animation from the update logic of the program itself.
3. Interaction with the external world - One other important functionality that is often overlooked is the capability to interact with the external world. In practice, animations are not just opaque objects that we simply run to completion, instead code using animations will often have aspects of the logic that are loosely dependent on the state of animation (we'll see some more examples of this in the case studies).

As such, it is important that the animation interface supports both:
- Animations communicating with external code:
- and external code communicating with animations:

In the rest of this section, we'll look at how to go about actually implementing these features.

Our game plan here will be in two phases:

First, we'll construct a simple functional DSL to represent timelines of transitions of values over time (interpolations, delays, etc.).
Then, in the second phase, we'll use algebraic effects to construct independent threads of control that switch between these transitions and communicate with the external world.

A functional DSL for timelines

Our datatype for transitions is as follows:

type t = MkState : {state:'a; update: 'a -> int -> 'a option} -> t

The idea here is that a transition consists of:

a persisted state for the transition
and an update function that takes the current state and the time and returns a new state or terminates.

Here, we use OCaml's existential types to allow different transitions to use different underlying states.

The update function for this data type is as you would expect:

let update (MkState {state;update}) time : t option =
  match update state time with
  | Some state -> Some (MkState {state; update})
  | None -> None

So, how do we use this?

Well, a good introductory example is in implementing a basic delay:

module Delay = struct
  let of_ delay =
    let update time delta = 
       let time = time + delta in
        if time < delay
            then Some time
            else None in
    MkState {state=0; update}
end

Here, the state of the transition is an integer representing the time that's elapsed, and each update just increments the elapsed time, terminating once the duration has been reached.

A slightly more interesting example is in the case of an interpolating transition, which gradually changes a variable from an initial value to a final value.

module Interpolate = struct

  let between ?(delay=100) set ~start ~stop  =
    let distance = stop - start in
    let update time delta =
      let time = time + delta in
      let proportion = Float.(of_int time / of_int delay) in
      if Float.(proportion > 1.0)
      then (set stop; None)
      else (set (start +. distance * proportion); Some time) in
    MkState {state=0; update}

end

Here, once again the state of the transition is an integer representing the elapsed time, but this time instead of just tracking the time, the transition will use a setter function to set the value of some arbitrary value each update.

Additionally, a nice benefit of making the transition updates functional is that they can compose quite nicely:

module Combine = struct
let in_parallel (MkState { state=s_a; update=u_a }) (MkState { state=s_b; update=u_b }) =
  let bind x f = match x with None -> None | Some v -> f x in
  let update (sa, sb) time =
    let sa = bind sa (fun v -> u_a v time) in
    let sb = bind sb (fun v -> u_b v time) in
    match sa, sb with
    | None, None ->
      (* a parallel animation completes when
         both constituents animations complete *)
      None
    | _ ->
      (* otherwise continue animation *)
      Some (o_sa, o_sb) in
  State.MkState {state=(Some s_a,Some s_b); update}

val in_sequence: Transition.t -> Transition.t -> Transition.t
end

Here, to run two transitions in parallel, we construct a new transition which tracks the state of both constituent animations and only terminates when both have completed. I've elided the definition of in_sequence for conciseness, however it follows mostly the same structure as parallel composition.

Overall, by combining these animations, we obtain quite a fluid interface for constructing complex transitions. However, our journey is not yet complete - as our transition data type currently represents a sort of reified encoding of an animation, alone they can be difficult to use and can easily be misused.

For example, suppose we construct an animation as follows:

let animate menu = 
   let update_brightness = 
        Interpolate.between ~start:0 ~stop:10 
        (fun v -> menu.brightness <- v) in
   let update_size = 
        Interpolate.between ~start:20 ~stop:30 
        (fun v -> menu.size <- v) in
   menu.selected <- next menu.selected;
   Combine.in_parallel
        update_brightness update_size

The problem here is that when constructing this animation,⁵ we set the value of the selected field on menu, however, this isn't done in during the animation, it is done at the time that the animation is constructed (which may not necessarily be the intention).

Indeed, to complete this animation interface, we must introduce one further level of composition.

Combining timelines into an animation

Finally we come to the algebraic effects part of this equation.

To start with, we'll construct a new effect specifically for animations.

effect Animation : Transition.t * (unit -> unit) option -> unit

Here our effect takes two parameters - 1. a transition to run, and 2. an optional function to be called when the animation is cancelled. For simplicity, we've made the effect return unit values, although one can image how we could modify the return type of the effect to allow more feedback between the execution of an animation and the external world.

As before, we'll construct another helper function to wrap the process of performing the effect:

let run ?on_cancellation (x: Transition.t) : unit = 
    perform (Animation (x, on_cancellation))

Now, we can pair this effect and the execution of animations into a data type that captures the execution of an animation:

type s = {
    current_state: Transition.t;
    kont: (unit, s) continuation option; 
    on_cancellation: (unit -> unit) option 
}

Here, an animation is represented as three components:

the currently executing transition
a continuation to resume the rest of the animation once the transition is complete
finally, an optional value to run if the animation is cancelled.

For the case of constructing a simple animation with no further continuation, we provide a helper:

let return (s: Transition.t) : s = { 
      current_state=s; 
      kont=None; 
      on_cancellation=None
   }

For type safety (and to avoid users accidentally raising unhandled effects), we'll create a newtype to distinguish between raw animations and complete animations:

type t = private s

With this, to construct a complete animation, we can use the following helper:

let build (f: unit -> s) : t =
  try f ()  with
  | effect (Animation (state, on_cancellation)) kont ->
    {current_state=state; kont=Some kont; on_cancellation}

The helper simply takes a function representing an animation and runs it until it either completes with a raw animation returns a final transition, or pauses its execution when an animation effect is performed.

Finally, once an animation is constructed, we can update it each iteration using a separate update function:

let update time (t: t) =
  match Transition.update t.current_state time with
  | Some state -> Some {t with current_state = state}
  | None -> match t.kont with
    | None -> None
    | Some kont ->
      Some (continue kont ())

The update function updates the current transition, and when it is complete, attempts to resume the rest of animation if it exists.

As we will see in the subsequent case studies, this interface allows for constructing complex animations fairly easily while also writing code in a direct and intuitive fashion.

Exploring the interface: Case studies

With this nice interface for animations at our hands, let's take it for a spin, and try making some interactive elements using it.

Let's start with our running example (and really the primary impetus for this post), the animated menu.

Note: In the rest of these examples, we will be assuming the existence of some kind of animation manager to handle tracking and updating animations. This can be implemented as basic hashtable mapping ids to animations and is fairly standard code, so I haven't included it in the post.

Animated Menu - Interleaving logic and animations

We'll start off by adapting the original type for our menu:

type t = {
  options: string list;
  mutable selected: int;
  mutable state: state;
}

Here, the main changes we've made are to introduce a new field to separately encapsulate the draw state⁶ and make certain fields mutable to account for the switch to an imperative style.

Unlike before, our new state type is now defined as follows, eliminating any details related to tracking the progress of animations:

type state =
  | Static                     (* drawing a static menu *)
  | Moving of {                (* draw a transition elements *)
      old_ind: int;
      old_brightness: int ref;
      current_brightness: int ref
    }

Here, this state parameter only tracks the information required to actually draw the menu - when drawing the menu, there are two main states:

a static menu - a single element of the menu is highlighted, and everything else is disabled.
a menu moving between states - the previously selected element of the menu fades out and the new selection fades in

I'll omit the actual draw code here because it's fairly straightforward and highly dependent on the graphics API.

The real magic of this system now comes in the update function, which is defined concisely as follows:

let update t status _time =
  match Graphics.key_pressed (), t.state with
  | false, _ 
  | _, Moving _ ->
    () (* if no key pressed or moving, ignore inputs *)
  | true, Static -> 
    (* if key pressed and in static state: *)
    let key = Graphics.read_key () in
    let len = List.length t.options in
    match key with
    (* move up *)
    | 'p' -> add_animation (change_index_anim t t.selected ((t.selected + 1) mod len))
    (* move down *)
    | 'n' -> add_animation (change_index_anim t t.selected ((t.selected - 1 + len) mod len))
    | _ -> ()

Notice how now the update function of the menu is separate from the logic for animations - the main change to the core logic is that when the user presses up and down, rather than immediately updating the state, we spawn a new animation to do it using the function change_index_anim:

let change_index_anim t start stop = Animation.build @@ fun () -> 
  let open Animation in
  let old_brightness = ref 100 in
  let current_brightness = ref 0 in
  (* update the state of the menu to be in a drawing state *)
  t.selected <- stop;
  (* run a transition that gradually changes the brightness of the old and new index *)
  t.state <- Moving {old_ind=start; old_brightness; current_brightness};
  run Transition.(
      Combine.in_parallel
        (Interpolate.between ~start:100 ~stop:0 ~delay:300
           (fun n -> old_brightness := n))
        (Interpolate.between ~start:0 ~stop:100 ~delay:300
           (fun n -> current_brightness := n)));
  (* after the transition completes, update the draw state of the menu to be static  *)
  t.state <- Static;
  return Transition.identity

Here this function builds an animation that gradually animates the colors of the old and new selected menu item. Notice that the animation logic itself is fully separated from the logic of the menu, only using the shared state field⁷ of the menu to communicate with the logic of the animation - for example, when the animation completes, it informs the core logic by setting the state variable to Static.

Combining these together, we obtain a smooth animated menu with little hassle:

Note: The version of the menu that is presented here is a slight simplification - the version in the codebase actually uses a more generic implementation that allows for type safe menu options.

Graph viewer - Using animations for logic

The menu was an example with fairly simple control flow and the skeptical reader may be worried that this animation interface might not scale to support more complex applications. To assuage such fears, our next example considers using this animation framework in implementing a slightly more complex example of an animated graph viewer, and we''l use this case study to explore how we can (ab)use animations to also perform some kinds of logic.

The idea with this application is that the user can use the interface to visually edit a graph, adding and moving vertices and edges.

To start, we'll set up the state of the application as follows:

type t = {
   graph: G.t;
   mutable state: state;
}

Here, G.t is just an instantiation of the imperative graph module provided by the venerable OCamlGraph library, with the individual vertices of the graph represented by the following type:

module Cell = struct 
type state = Static | Growing

type t = {
  data: string; 
  mutable x: int; mutable y: int;
  mutable width: int; mutable height: int;
  mutable state:state;
}
end

Here, as cells themselves are also animated, we have this additional parameter to track whether the cell is static or growing.

The state of the main application is then defined as follows:

type state = View | Move of Cell.t | EdgeStart | EdgeFirst of Cell.t | Insert | Debounce

Here, we've identified 5 main states that capture the core logic of the program:

View mode - the default mode in which no logical operation is pending
Move mode - when the user has continued to click on a particular node and is now moving it around
Edge Mode (start) - the mode used to insert edges
Edge mode (first) - the mode used to insert edges after the user has clicked on an initial node to start the edge from
Insert mode - A mode used to insert new nodes into the graph

We also include this one additional node, Debounce, which doesn't correspond directly to a logical state, but is used as a quality of life feature to debounce inputs by abusing animations.

Once again, drawing the graph is fairly straightforward, and just consists of iterating through the edges and vertices and drawing them to screen. The interesting part of this implementation is in the update function:

let update viewer s _time =
  (* find cell containing mouse if exists *)
  let screen_mouse_pos = Coordinate_system.from_display (s.mouse_x,s.mouse_y) in
  let cell_contains = find_cell_at_point screen_mouse_pos in
  match viewer.state with
  | View -> ...               (* handle view mode *)
  | Debounce -> ()            (* in debounce mode, ignore inputs *)
  | EdgeStart -> ...          (* handle edge mode (start) *)
  | EdgeFirst cell -> ...     (* handle edge mode (first)  *)
  | Insert -> ...             (* handle insert mode *)
  | Move cell ->              (* handle move mode *)

As this more complex application, the update function is probably too large to cover in its entirety in this blog post (~30 lines overall), so instead, we'll focus in on few of the most interesting cases of the implementation.

View mode
The view mode is the default mode the user is in, used to view the overall graph - as such it doesn't have any specific functionality of its own, and its update code is mainly concerned with swapping to other states:
```
| View ->
  begin match cell_contains, Graphics.button_down () with
    | Some cell, true -> set_to_state viewer (Move (cell))
    | _ -> match Graphics.key_pressed (), Graphics.read_key () with
      | true, 'e' -> set_to_state viewer EdgeStart
      | true, 'i' -> set_to_state viewer Insert
      | _ -> ()
  end
```
Here, the update function is fairly straightforward - if the user has clicked on a particular node, then we transition to the move state, and otherwise if the user has pressed a key corresponding to one of the other modes, then we transition.

In all cases, in order to implement the transition, we use an auxiliary function set_to_state to actually perform the change.

As one might expect, this function actually works by means of delegating to animations:
```
let debounce_to viewer ~stop ~delay = Animation.build @@ fun () -> 
  let open Animation in
  viewer.state <- Debounce;
  run Transition.(Delay.of_ ~delay);
  viewer.state <- stop;
  return Transition.identity

let set_to_state viewer =
  add_animation (debounce_to viewer ~stop:st ~delay:100)
```
Here, in order to change the state of the application, we spawn a new animation that first sets the state of the application to the special debounce state, and then only after a certain delay does the state finally change to the desired one.

The idea with this transition sequence is to avoid the user accidentally invoking multiple events - whenever a transition occurs, there is a small debouncing period where the application ignores all inputs.

In some sense, this could be considered an abuse of animations, but given that it isn't directly related to the core logic of the application, this seems like an ideal use of the interface.

Insert mode

Another interesting case is that of the insert mode which is used to insert new nodes:

| Insert -> 
  begin match cell_contains, Graphics.button_down () with
    | None, true ->
      let cell = create_cell screen_mouse_pos (Random.run (List.random_choose strings)) in
      G.add_vertex graph cell;
      set_to_state Insert
    | _ -> match Graphics.key_pressed (), Graphics.read_key () with
      | true, 'e' -> set_to_state viewer EdgeStart
      | true, 'i' -> set_to_state viewer View
      | _ -> ()
  end

Once again, thanks to the animations, the logic of this case is fairly straightforward and easy to follow: the application first checks if the user has clicked on a region that is not occupied by any other cell, and if so, spawns a new cell at that position. Otherwise, the application just checks if the user has pressed a button for another state.

The interesting part is in the create_cell operation, which handles creating a new vertex of the graph and its animation:

let create_cell_animation cell  = Animation.build @@ fun () -> 
  let open Animation in
  cell.state <- Growing;
  run Transition.(Combine.in_parallel
                    (Interpolate.between ~start:0 ~stop:200 ~delay:200
                       (fun n -> cell.width <- n))
                    (Interpolate.between ~start:0 ~stop:100 ~delay:200
                       (fun n -> cell.height <- n)));
  cell.state <- Cell.Static;
  return Transition.identity

let create_cell (x,y) txt =
  let cell = Cell.{
      data=txt; x;y;
      width=0; height=0;
      state=Static;
    } in
  add_animation (create_cell_animation cell);
  cell

Here, when a vertex is created, we also spawn a new animation that gradually grows the cell from nothing to its final dimension creating a more fluid interface.

Overall application

Combining all the components together, we can manage the complex logic of the underlying application while still being able to make use of animations:

Bouncing balls - Complex animations (infinite and resumable)

Switching gears again, our final case study now swaps the focus from complex application logic to a more complex animation flow. In this simple program, we'll construct a small playground of bouncing balls, each of which can be manipulated by the user (dragged around, stopped etc.) using their mouse.

First, we'll construct a simple data structure to represent the state of an individual ball in the program:

module Circle = struct
   type state = Stationary | Moving | Squashed

   type t = {
      mutable state: state;
      mutable x: int; mutable y: int;
      mutable w: int; mutable h: int;
   }
end

Here, as the balls themselves will be individually animated, we keep an additional state to track the status of the ball - either it is stationary, moving or squashed.

type state = None | Hover of Circle.t * Animation.t | Clicked of Circle.t
type t = {
  mutable circles: Circle.t list;
  mutable state: state;
  mutable selected: bool;
}

The state of the overall program this time is split into three different cases:

None - No ongoing interaction by the user
Hover - User is hovering over a given circle and has paused its animation
Clicked - User has clicked and is dragging a circle

As is par for the course, I'll omit the drawing function here, and we'll focus straight on the update operation:

let update game s _time =
  let circle_at_mouse = find_circle_at_mouse game.circles s.mouse_x s.mouse_y in
  let mouse_down = Graphics.button_down () in
  match game.state, circle_at_mouse with
  (* Case 1: hovering on circle  *)
  | None, Some circle ->                        
    let anim = remove_animation circle in
    game.state <- Hover (circle, anim)
  (* Case 2: Clicking on circle *)
  | Hover _, Some circle when mouse_down && not game.selected ->
    game.state <- Clicked circle;
    game.selected <- true;
  (* Case 3: leaving hovering circle *)
  | Hover (circle, anim), None ->
    add_animation circle anim;
    game.state <- None
  (* Case 4: releasing click on circle *)
  | Clicked circle, _ when not mouse_down ->
    add_animation circle (circle_bounce_anim circle);
    game.selected <- false;
    game.state <- None;
  (* Case 5: dragging circle *)
  | Clicked circle, _ ->
    circle.x <- s.mouse_x;
    circle.y <- s.mouse_y;
  | _ -> ()

Here the code is fairly straightforward, and the logic is implemented by means of a straightforward case analysis of the 5 possible logical states the application could be in:

When the user first hovers on a circle, the animations for the circle are paused and the application switches to the hovering state.
When the user clicks on a circle they are selecting, the application switches to the clicked state
When the user leaves the region of a circle they were hovering in, the application resumes the animation of the circle and switches state to None.
When the user releases a click on a circle they were dragging, the application starts a new animation for the circle (using circle_bounce_anim) and then switches state to None
When the user drags a circle, then the position of the circle is updated accordingly.

A nice feature of this example is that it highlights how well the animation interface allows for the logic of the application to be fully decoupled from the animation - in fact, we can even pause and resume animations at will.

The other interesting part of this case study is the actual animation function circle_bounce_anim, which unlike the previous animations we've considered is not a finite animation, but rather infinitely repeating. The beauty of this interface is that we are able to achieve this behaviour without having to write any additional code.

So how do we do it?

Well, as algebraic effects allow us to embed our animations directly within direct style code, an infinite animation is simply an infinite loop:

let circle_bounce_anim circle = 
  let rec loop () = 
    let open Animation in
    (* move circle down *)
    circle.state <- Moving;
    run Transition.(Interpolate.between ~start:circle.y ~stop:(circle.y - 200) ~delay:300
                      (fun y -> circle.y <- y));
    (* squash circle  *)
    circle.state <- Squashed;
    (* first, squash out *)
    run Transition.(Combine.in_parallel
                      (Interpolate.between ~start:circle.w ~stop:(circle.w + 30) ~delay:100
                         (fun y -> circle.w <- y))
                      (Interpolate.between ~start:circle.h ~stop:(circle.h - 30) ~delay:50
                         (fun y -> circle.h <- y)));
    (* then return back to original shape *)
    run Transition.(Combine.in_parallel
                      (Interpolate.between ~start:circle.w ~stop:(circle.w - 30) ~delay:120
                         (fun y -> circle.w <- y))
                      (Interpolate.between ~start:circle.h ~stop:(circle.h + 30) ~delay:80
                         (fun y -> circle.h <- y)));
    (* move circle up *)
    circle.state <- Moving;
    run Transition.(Interpolate.between ~start:circle.y ~stop:(circle.y + 200) ~delay:300
                      (fun y -> circle.y <- y));
    (* pause at apex of curve *)
    circle.state <- Stationary;
    run @@ Transition.(Delay.of_ ~delay:50);
    (* run animation again *)
    loop () in
  Animation.build loop

Here, the circle bouncing animation is written as a straightforward intuitive loop that just directly iterates over each stage of the animation of the ball - first it falls downards, then it squashes, and then it bounces back up. Once the animation is complete, it just loops again. Once again, notice how the animation code is completely decoupled from the logic of the actual application.

Combining these all together, we then round off our case study exploration with a final dynamic animation of these bouncing balls:

Aside: Why not FRP?

Before I wrap up this post for real, I should answer one particular question that might be on your mind: why not functional reactive programming?

Functional reactive programming (FRP) is a somewhat de-facto approach for encoding animations in a functional style - almost any search for animations and functional programming will almost always produce results about FRP.

The general idea of FRP is to encode your overall animation as a sort of dependency graph, where the vertices in the graph represent values that vary over time and the edges in the graph represent data dependencies between these values - i.e if a variable A is dependent on another variable B, then when B updates the value of A must also update.

In FRP lingo, a time varying continuous value is a signal, and a discrete one is an event:

type 'a signal                 
type 'a event

For example, if you wanted to draw a picture at the coordinates of your mouse, this could be done by constructing the picture itself from the "node" in the dependency graph representing the position of the mouse.

val mouse_position: (int * int) signal

let drawing : circle signal = 
       Signal.map (fun (x,y) -> Circle (x,y)) mouse_position

By its nature, FRP meshes quite well with the monadic approach - the construction of these dependencies essentially becomes a reified representation of your animation (similar to the timeline structure we saw earlier) and its construction can be simplified using monad binding.

Now, the core problem that I have with FRP is the infectious nature of its encoding - when constructing animations, if any value in your program happens to be dependent on a time varying value, then FRP requires that it must also be encoded into the dependency graph - so the general idea here would be that your overall application/game would eventually just end up being a single time varying representation of the state of the game.

As one might imagine, this can quickly become quite annoying. For example, in order to introduce animations into your code - even if these animations are just for a small part of the program, you are still forced to wrap the entire program into this paradigm. While this kind of obsessive adherence to propagating monadic wrappers throughout a codebase might be more palatable if coming from a Haskell background, in general, one of the niceties of idiomatic OCaml is that it is usually a lot more practical - hence why I opted not to go for FRP.

Conclusion: Now Algebraic effects are my best friend

Finally, we come to the end of this long post. Hopefully, over the course of these case studies, I've managed to convince you of the fluidity and ease of use of this algebraic-effects-powered interface to animations.

While strictly-speaking the functionality of algebraic effects used in this post can be mostly replicated using existing control flow constructs, I really found that the mindset of explicitly managing continuations brought on through algebraic effects really helped in coming up with this interface.

If nothing else, the issue of mixing logic and animation code has been one that has been plaguing me for quite a while, and I haven't really seen many posts about how this can be managed,⁸ so hopefully this might be of use to someone else.

Overall, I found the process of working with algebraic effects to be pleasing and open up a huge variety of novel patterns for approach problems in OCaml and I'm eagerly looking forward to what new developments may be made on this front in the coming year.

Footnotes

If you are familiar with monads, I am referring here to a free monad.

Amongst many other benefits.

I should note that the code used in the blog post has been cleaned up a bit and adjusted to fit the narrative, although the core ideas are still the same.

⁴

Or if you are familiar with delimited continuations such as shift/reset, algebraic effects are essentially a nicer structured form of these operations.

⁵

In this example the mistake is quite obvious, however in practice, typically this kind of interface is provided alongside a monadic interface, and in such instances, it can be easy to accidentally write imperative code that will be run at construction time rather than during the execution of the animation.

⁶

If you look at our original formation, the state parameter tracked both the selected value and the animation state, while here the logical components of the menu are isolated from the state required for drawing.

⁷

This shared state would still be achievable in a pure setting - the difference would be that the menu state would have to be explicitly passed to the update function of both the animations and the menu itself. It would require a bit more type scaffolding but this would still be achievable in a type safe way.

⁸

I've even looked at the source code of a couple of popular Haskell games, but I've found that these games don't often rely on complex animations or use logic that is dependent on animations completing.